一大堆算法题。

[TOC]

1. 贪心法

1.1 快乐司机

题目描述

“嘟嘟嘟嘟嘟嘟

喇叭响　　我是汽车小司机　　我是小司机　　我为祖国运输忙　　运输忙”

这是儿歌“快乐的小司机”。话说现在当司机光有红心不行，还要多拉快跑。多拉不是超载，是要让所载货物价值最大，特别是在当前油价日新月异的时候。司机所拉货物为散货，如大米、面粉、沙石、泥土……

现在知道了汽车核载重量为w，可供选择的物品的数量n。每个物品的重量为gi,价值为pi。求汽车可装载的最大价值。

输入格式

输入第一行为由空格分开的两个整数 n w

第二行到第n+1行，每行有两个整数，由空格分开，分别表示gi和pi

输出格式

最大价值（保留一位小数）

样例

样例输入

样例输出

71.3

数据范围与提示

解释：

先装第5号物品，得价值35，占用重量7
再装第4号物品，得价值36.346,占用重量29
最后保留一位小数，得71.3

范围

（n<10000,w<10000,0<gi<=100,0<=pi<=100)

代码

#include<iostream>
#include<algorithm>
using namespace std;
struct goods
    {
        float weight;   // 重量 定义为float类型 整型/单精度 = 单精度
        int prices;   // 价值
        float unit_value;   //单位价值
    }commodity[10000];
// 自定义排序规则
bool com(const goods &a,const goods &b)
    {
     //结构体排序  按单位价值 unit_value 升序 
     return a.unit_value>b.unit_value;
    }
int main(){
    int n,w;
    float sum = 0;
    cin >> n >> w;
    for (int i = 0; i < n; i++)
    {
        cin >> commodity[i].weight >> commodity[i].prices;
        commodity[i].unit_value = commodity[i].prices / commodity[i].weight;
    }
    sort(commodity,commodity + n,com);  // 给数组排序
    /*   调试代码
    for (int j = 0; j < n; j++)
    {
        cout << commodity[j].unit_value << endl;
    }  */

    for (int i = 0; i < n && w > 0; i++)
    {
        if (w >= commodity[i].weight)
        {
            sum = sum + commodity[i].prices;
            w = w - commodity[i].weight;
        }
        else{  // 如果可以装载的重量 w < 物品的重量 则只能再装载一个货物的一部分
               // sum就等于剩余的装载量 w * 物品的单位价值
            sum = sum + w * commodity[i].unit_value; 
            w = 0;   //装载量归零
        }
    }
   // cout << sum << endl;   c++的输出精度太高
    printf("%.1f",sum);
    return 0;
}

1.2 活动安排

输入格式

第一行一个整数 nn；

接下来的 nn 行，每行两个整数 s_is**i 和 f_if**i。

输出格式

输出互相兼容的最大活动个数。

样例

输入样例 1

输出样例 1

数据范围与提示

1≤n≤1000

代码

#include<iostream>
#include<algorithm>
using namespace std;
//定义结构体 存储每个活动的开始和结束时间
struct act_time
{
    int start;
    int end;
}act[1000];

//自定义排序
bool com(const act_time &a,const act_time &b)
   {   //降序
    return a.start < b.start;  
   }
int main(){
    int n;
    int count = 1;   //默认第一个直接安排
    int m = 0;
    cin >> n;
    for (int i = 0; i < n; i++)
    {       
        cin >> act[i].start >> act[i].end;
    }
    sort(act,act+n,com);   //按照start由小到大的顺序排序
    
    // for (int i = 0; i < n; i++)
    // {
    //     cout << act[i].start << endl;
    // }
    
    for (int j = 1; j < n; j++)
    {   
        if (act[j].start >= act[m].end)   //后续活动的开始时间 >= 上一个被安排的活动的截止时间
        {   
            m = j;    //记录被安排的活动的下标
            count++;
        }
    }
    cout << count << endl ;
}

1.3 分发饼干

题目描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

输入格式

第一行两个数，分别表示孩子个数和饼干块数第二行输入各孩子的胃口值第三行输入饼干的尺寸

输出格式

被满足的孩子的个数

样例

样例输入 1

1
2
3

3 2
1 2 3
1 1

样例输出 1

样例输入 2

1
2
3

4 4 
10 9 8 7
5 6 7 8

样例输出 2

数据范围与提示

1 <= g.length <= 3 * 104 0 <= s.length <= 3 * 104 1 <= g[i], s[j] <= 231 - 1

代码

#include<iostream>
#include<vector>
#include<limits.h>
#include<algorithm>  //这个头文件包含sort方法
using namespace std;
const int N = 1000;

int main(){
    int children[N];
    int cookie[N];
    int count = 0;   //用来统计满足的孩子
    int coo = 0;
    int chi = 0;
    
    cin >> chi >> coo;
    for (int i = 0; i < chi; i++)
    {
        cin >> children[i];
    }
    for (int j = 0; j < coo; j++)
    {
        cin >> cookie[j];
    }
    
    
    sort(children, children + chi);  //按从小到大排序 让小饼干去遍历所有孩子
    sort(cookie, cookie + coo);
    
    int i = 0;
    int j = 0;
    while (i < coo)
    {
        if(cookie[i] >= children[j]){
            count++;
            i++;
            j++;
        }else{
            i++;
        }
    }
    cout << count << endl;
    return 0;
}

2. 蛮力法

2.1 狱卒问题

题目描述

某王国对囚犯进行大赦,让一狱吏n次通过一排锁着的n间牢房,每通过一次按所定规则转动门锁,每转动一次,原来锁着的被打开,原来打开的被锁上；通过n次后,门锁开着的,牢房中的犯人放出,否则犯人不得获释.转动门锁的规则是这样的,第一次通过牢房,要转动每一把门锁,即把全部锁打开；第二次通过牢房时,从第二间开始转动,每隔一间转动一次；第k次通过牢房,从第k间开始转动,每隔k-1 间转动一次；问通过n次后,那些牢房的锁仍然是打开的?

输入格式

一行一个整数n

输出格式

用空格隔开每个数字

样例

输入样例1

输出样例1

1 4

输入样例2

输出样例2

1	1 4 9 16 25

数据范围与提示

n<=1000

代码

#include <stdio.h>
#include <stdlib.h>
 
int main(){
    int n = 0;
    int i = 0;
    int j = 0;
    int *p = NULL;
    scanf("%d",&n);
    p =(int *)calloc(n+1,sizeof(int));

    //设置牢房的初始状态 默认1为上锁 0为解锁
    for (i = 1; i <= n; i++)
    {
        /* code */
        p[i] = 1;
        
    }
    for (i = 1; i <= n; i++)
    {
        /* code */
        for (j = i; j <= n; j+=i)   //间隔 i个
        {
            /* code */
            // 转动锁
            p[j] = 1 - p[j];
            
        }
        
    }
    for (i = 1; i <= n; i++)
    if(p[i] == 0)
    {
        printf("%d被释放了\n",i);
        
    }
    free(p);
    return 0;

    
    
}

2.2 四平方和

题目描述

四平方和定理，又称为拉格朗日定理：每个正整数都可以表示为至多4个正整数的平方和。如果把0包括进去，就正好可以表示为4个数的平方和。

比如：5 = 0^2 + 0^2 + 1^2 + 2^25=02+02+12+22，7 = 1^2 + 1^2 + 1^2 + 2^27=12+12+12+22

对于一个给定的正整数，可能存在多种平方和的表示法。要求你对4个数排序：0 <= a <= b <= c <= d。并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法

输入格式

一个正整数N (N<5000000)

输出格式

4个非负整数，按从小到大排序，中间用空格分开

样例

样例输入 1

样例输出 1

0 0 1 2

样例输入 2

样例输出 2

0 2 2 2

样例输入 3

样例输出 3

1	1 1 267 838

代码

#include <stdio.h>
#include <math.h>

int main(){
    int n;
    scanf("%d",&n);
    for (int i = 0; i < 2300; i++)
    {
        for (int j = 0; j < 2300; j++)
        {
            /* code */
            for (int p = 0; p < 2300; p++)
            {
                /* code */
                int a = sqrt(n - i*i - j*j -p*p);
                if (i*i+j*j+p*p+a*a == n)
                {
                    printf("%d %d %d %d",i,j,p,a);
                    return 0;
                }
                
            }
            
        }
        
    }
    
}

2.3 求n以内的所有素数

输入格式

一行，输入一个数n

输出格式

分行输出n以内的所有素数

样例

输入样例

输出样例

1
2
3

2
3
5

代码

#include <stdio.h>

int main(){
    int i,j,n;
    scanf("%d",&n);
    for ( i = 2; i <=n; i++)
    {
        /* code */
        for ( j = 2; j < i; j++)
        {
            /* code */
            if (i%j == 0)
            {
                /* code */
                break;
            }
            
        }
        if (j == i)
        {
            /* code */
            printf("%d\n",i);
        }
        
        
    }
    
}

2.4 找零问题

题目描述

有n个人正在饭堂排队买海北鸡饭。每份海北鸡饭要25元。奇怪的是，每个人手里只有一张钞票（每张钞票的面值为25、50、100元），而且饭堂阿姨一开始没有任何零钱。请问饭堂阿姨能否给所有人找零（假设饭堂阿姨足够聪明）,n不超过1000000

输入格式

第一行一个整数n，表示排队的人数。

接下来n个整数a[1],a[2],…,a[n]。a[i]表示第i位学生手里钞票的价值（i越小，在队伍里越靠前）

输出格式

输出YES或者NO

样例

样例输入1

1 2	4 25 25 50 50

样例输出1

YES

样例输入2

1
2

2
25 100

样例输出2

NO

样例输入3

1 2	4 25 25 50 100

样例输出3

YES

代码

#include<iostream>
using namespace std;

int main(){
    bool count = 0;
    int bill_25, bill_50, bill_100 = 0;  //初始化阿姨手中各个面值的钱
    int n = 0;
    cin >> n;
    int money[1000001];
    for (int i = 0; i < n; i++)
    {
        cin >> money[i];
    }

    if (money[0] != 25)   //如果第一个不是收到25 则直接输出 no
    {
        cout << "NO" << endl;
    }else{
        count = 1;  //1表示可以找开 0 表示不行
        for (int i = 0; i < n; i++)
        {
            if (money[i] == 25)
            {
                bill_25++;
            }else if (money[i] == 50)
            {
                bill_50++;
            }else
                bill_100++;
            money[i] = money[i] - 25;   //学生的钱 - 25 = 要找的钱
            if (money[i] == 75 && bill_50 != 0)
            {
                money[i] = money[i] - 50;
                bill_50--;
            }
            while (money[i] > 0 && bill_25 >= 0)
            {
                money[i] = money [i] - 25;
                bill_25--;
            }
            if (money[i])  //如果money[i]的值不等于 0 则说明找不开
            {
                count = 0;
                break;
            }  
        }
        if (count)
        {
            cout << "YES" << endl;
        }else{
            cout << "NO" << endl;
        }
           
    }
    return 0;
}

2.5 最长公共子串

题目描述

这是一道模板题。

给定 nn 个字符串，试求出这些字符串的最长公共子串。

输入格式

第一行一个整数 nn。

下面第 22 到 n+1n+1 行，每行一个字符串。

输出格式

仅一行，包含一个正整数，表示 nn 个字符串的最长公共子串长度。

样例

输入样例 1

1
2
3

2
ababc
cbaab

输出样例 1

数据范围与提示

对于第 ii 个测试点，保证 n,=,i+1n=i+1。

对于每一个字符串，保证 |str|,\le,10^{\lceil \frac{i}{3}\rceil}∣str∣≤10⌈3i⌉，出现字符均为小写英文字母。

代码

#include<iostream>
#include<cstring>
using namespace std;


int main(){
    int n;  //输入的串数
    cin >> n;
    char str[255][255];  //用来保存所有字符串
    int Len[n];       //这个数组用来保存每个字符串的长度
    int minString = 0;   //保存最短的字符串所在的行号
    int minLen = 255;    //保存最短的字符串的长度
    int count = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> str[i];
        Len[i] = strlen(str[i]);
        if (minLen > Len[i])
        {
            minLen = Len[i];
            minString = i;
        }

    }
    char pice_string[255];   //pice_string[]表示字符串的片段 
    //memset(pice_string, '\0' , sizeof(pice_string));   //初始化数组 填充 '\0'
    for (int i = 0; i < minLen; i++){
        for(int j = 1; j <= minLen-i; j++){
            strncpy(pice_string, str[minString] + i, j);    //获取最短的字符串的片段 复制到 pice_string中
            pice_string[j] = '\0';
            //cout << pice_string << endl;
            bool flag = true ;
            for (int m = 0; m < n; m++)
            {
                if (strstr(str[m], pice_string) == NULL)   //用strstr()判断二维素组的每一行是否含有 pice_string公共串
                {
                    flag = false;   //如果没有则证明 不是公共子串
                    break;
                }
                
            }
            if (flag && strlen(pice_string) > count )   //如果有更长的公共串则替换
            {
                count = strlen(pice_string);
            }
            
            
        }  
    }
    cout << count << endl;
    return 0;
}

3. 分治法

3.1 最大子段和

题目描述

给出一个长度为n的整数列a，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度n; 第二行有n个整数，第i个整数表示序列的第i个数字a_ia**i

输出格式

输出一行一个整数表示答案：最大子段和的值。

样例

样例输入

1 2	6 -2 11 -4 13 -5 -2

样例输出

数据范围与提示

n<=100

代码

#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;

 int main() //动态规划
{   int n,i; 
    cin >> n;
    vector<int> second_in(n);  // 存储输入的数据
    vector<int> ans(n);        // 存储当前的最大子段和
    for(i = 0;i < n;i++) 
    {
        cin >> second_in[i];
    }
    ans[0] = second_in[0];
    for(i = 1;i < second_in.size();i++)
    {   // 采用循环的方式 将前几项的+当前项的和 与当项进行比较 取最大值
        // 将两者中大的值赋给 ans[i] 存储
        ans[i] = max(ans[i-1]+second_in[i],second_in[i]); 
    }
    cout << *max_element(ans.begin(),ans.end()) << endl;
	
	return 0;
}

3.2 股票买卖算法

题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

输入格式

一个数字，表示总天数一行数字，表示某几天购入该股票的价格

输出格式

一个数字，表示能获取的最大利润

样例

输入样例 1

1 2	6 7 1 5 3 6 4

输出样例 1

代码

#include<iostream>
#include<limits.h>
using namespace std;
int maxEarning(int* prices,int len){
    int sum = 0;
    int low = INT_MAX;
    for (int i = 0; i < len; i++)
    {
        /* code */
        //贪心算法 后一天比前一天价格高 就买入
        low = min(low,prices[i]);  //在第i天之前买入的最低价格
        sum = max(sum,prices[i] - low);  //prices[i]-low表示在第i天卖出能获取的利润
    }
    return sum;
};
int main()
{   int len ;
    int i = 0;
    char c;
    cin >> len;
    int prices[len];
    while (len > i)
    {
        /* code */
        c = getchar();
        ungetc(c,stdin);  //ungetc()获取一个字符并将其推回到流中，以便可以再次读取该字符
        cin>> prices[i++];
    }
    cout << maxEarning(prices, len) << endl;
    return 0;
}

3.3 二分查找

题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。

输入格式

两行。第一行输入两个整数n,kn,k，nn表示数组的长度，kk表示要查找的目标值；第二行输入一个长度为nn的有序数组。

输出格式

一行，输出kk的索引，如果没有找到kk，则输出-1−1。

样例

样例输入 1

1 2	10 6 1 2 3 4 5 6 7 8 9 10

样例输出 1

样例输入 2

1 2	4 5 1 3 5 6

样例输出 2

代码

#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;
int bi_find(vector<int > &arr,int value){
    int l=0,r=arr.size()-1,mid;
    while(l<=r){
        mid=l+(r-l)/2;
        if(arr[mid]==value) return mid;
        
		if(arr[mid]<value) l=mid+1;
        else if(arr[mid]>value)  r=mid-1;

    }
    return l;
}
int main(){
    int n,i,value;
    cin>>n>>value;
	vector<int> arr(n);
	
	for(i=0;i<n;i++){
		cin>>arr[i];
	}
	cout<<bi_find(arr,value);




    return 0;
}

3.4 二分查找进阶

题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

输入格式

两行。第一行输入两个整数n,kn,k，nn表示数组的长度，kk表示要查找的目标值；第二行输入一个长度为nn的有序数组。

输出格式

一行，输出kk的索引，如果没有找到kk，则输出返回它将会被按顺序插入的位置。

样例

样例输入 1

1 2	4 5 1 3 5 6

样例输出 1

样例输入 2

1 2	4 2 1 3 5 6

样例输出 2

代码

#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;
int half_find(vector<int > &arr, int key){
    int l = 0, r = arr.size()-1, mid;      // l为下界 r为上界 mid为居中元素
    while(l <= r){        
        mid= l + (r-l)/2;
       if(arr[mid] == key) {   
            return mid;     //首先验证是否是居中的元素，如果是，那么那么直接返回
        }    
		if(arr[mid] < key){
            l = mid + 1;    //如果大于居中元素，则修改查找下界为居中元素右侧的元素
        } 
        else if(arr[mid] > key){
            r = mid - 1;    //如果小于居中元素，则将查找上界修改为居中元素左侧的元素 
        } 
    }
    return l;               //如果数组中没有这个数 则返回下届l 即它的插入位置
}
int main(){
    int n, i, key;
    cin >> n >> key;
	vector<int> arr(n);
	for(i = 0;i < n; i++){
		cin >> arr[i];
	}
	cout << half_find(arr,key) << endl;
    return 0;
}

3.5 二分查找数组元素

题目描述

用递归函数实现二分法查找数组元素。补充：要求给定数组采用如下代码定义 int data[200]; for (i=0; i<200; i++） data[i]=4*i+6;

输入格式

输入一个待查找的整数（该整数一定在数组data中）

输出格式

该整数在数组中的指标

样例

样例输入 1

样例输出 1

样例输入 2

样例输出 2

样例输入 3

样例输出 3

数据范围与提示

输入数据中每一个数的范围。输入数据必须满足4*i＋6，i＝0,1,2,3,…,198,199

代码

#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;

int half_find(int data[],int key,int min,int max){
    int half = (min + max) / 2;
    if (min > max)
    {
        return -1;  
    }
    if (key == data[half])
    {
        return half;
    }
    //如果目标值<中间位置的值 则在（min，half-1）区间继续查找
    else if (key < data[half])
    {  //递归调用
        return half_find(data,key,min,half - 1);  
    }
    else
        return half_find(data,key,half + 1,max);
}

int main(){
    int key;   //目标值
    int data[200];
    for (int i = 0; i < 200; i++)
    {
        data[i] = 4 * i + 6;  //初始化数组
    }
    cin >> key;
    cout << half_find(data,key,0,200);
    return 0;
}

3.6 高精度乘法

题目描述

给定两个正整数A和B，请你计算A * B的值。

输入格式

共两行，第一行包含整数A，第二行包含整数B。

输出格式

共一行，包含A * B的值。

样例

输入格式

1
2

4
6

输出格式

数据范围与提示

1≤A的长度≤100000, 0≤B≤10000

代码

#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;
int main(){
	string num1, num2;
	int sum[100010] = {0};
	cin >> num1 >> num2;
		if(num1[0] == '0'||num2[0] == '0'){
		cout << 0;
		return 0;
	}
	for(int i = num1.size() - 1; i >= 0; i--){
		for(int j = num2.size() - 1; j >= 0; j--){          // num[]是字符串数组 - ‘0’将它转换为整型数组 从而进行乘法运算
			sum[num1.size() + num2.size() -  j - i - 2] += (num1[i] - '0')*(num2[j] - '0');
		}
	}
	for(int i = 1; i < 100010; i++){
		sum[i] += sum[i-1]/10;    // 满10进位
		sum[i-1] = sum[i-1]%10;   // 对原来的数取余
	}
		for(int i = 100010-1; i >= 0; i--){
		if(sum[i] != 0){
			for(;i >= 0;i--) cout << sum[i];
			return 0;
		}
	}	
	return 0;
}

3.7 棋盘覆盖问题

题目描述

在一个2^k \times 2^k2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型3格板覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型3格板不得重叠覆盖。求解覆盖方案。

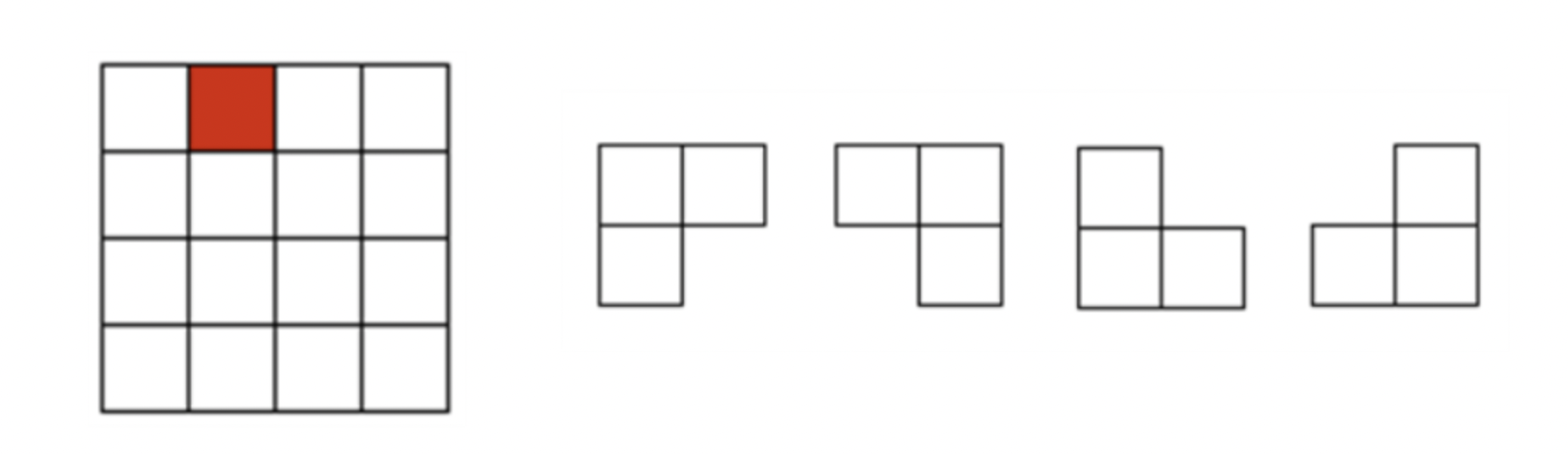
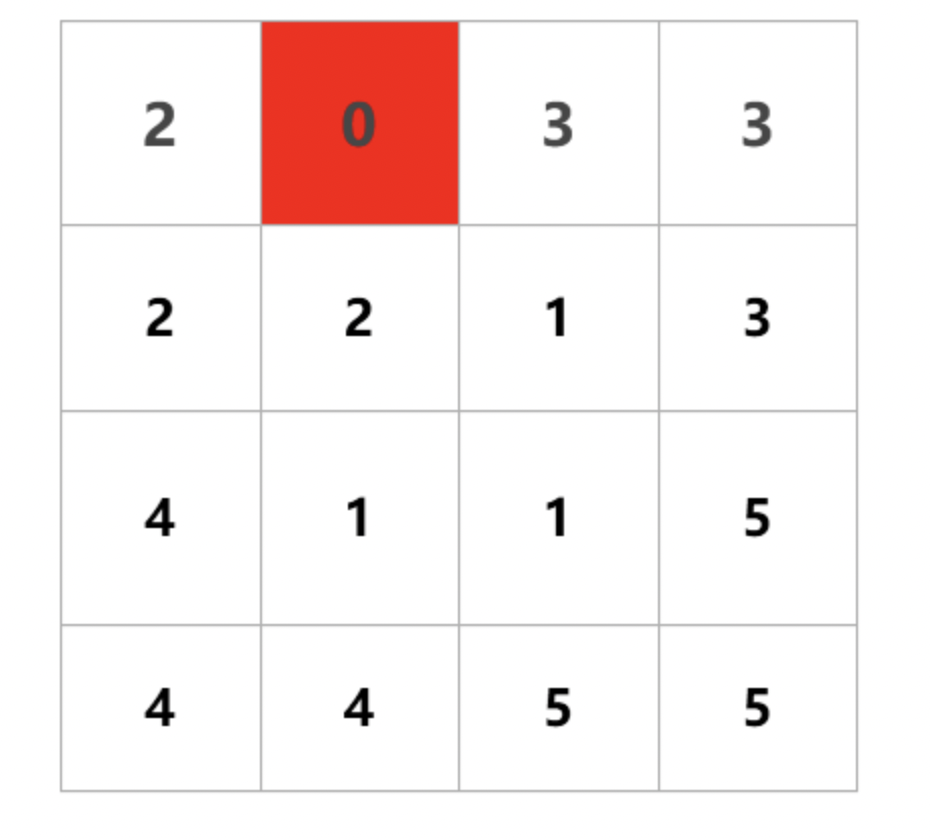
当k=2；特殊方格位于第0行，第1列的一种求解方案。

输入格式

输入三个整数例如： 2 0 1 分别代表k值，特殊方格所在行，特殊方格所在列

输出格式

模拟棋盘的二维数组每一位元素，每个元素占3个字符位置。例如printf(“%3d”,board[i][j]);

样例

样例输入

2 0 1

样例输出

代码

#include<iostream>  
#include<stdio.h>
using namespace std;  
int tile=1;                   //L型骨牌的编号(递增)  
int board[100][100];  //棋盘  
 
//递归方式实现棋盘覆盖算法  
// tr--当前棋盘左上角的行号 
// tc--当前棋盘左上角的列号 
//dr--当前特殊方格所在的行号 
// dc--当前特殊方格所在的列号 
//size：当前棋盘的:2^k 

void chessBoard (int tr, int tc, int dr, int dc, int size)  
{  
    if(size == 1)    //棋盘方格大小为1,说明递归到最里层  
        return;  
    int t = tile++;     //每次递增1  
    int s = size/2;    //棋盘中间的行、列号(相等的)  
    //检查特殊方块是否在左上角 子棋盘 中  
    if(dr<tr+s && dc<tc+s )              //在  
        chessBoard(tr, tc, dr, dc, s);  
    else         //不在，将该子棋盘右下角的方块视为特殊方块  
    {  
        board[tr+s-1][tc+s-1] = t;  
        chessBoard(tr, tc, tr+s-1, tc+s-1, s);  
    }  
    //检查特殊方块是否在右上角子棋盘中  
    if(dr<tr+s && dc>=tc+s)               //在  
        chessBoard(tr, tc+s, dr, dc, s);  
    else          //不在，将该子棋盘左下角的方块视为特殊方块  
    {  
        board[tr+s-1][tc+s] = t;  
        chessBoard(tr, tc+s, tr+s-1, tc+s, s);  
    }  
    //检查特殊方块是否在左下角子棋盘中  
    if(dr>=tr+s && dc<tc+s )              //在  
        chessBoard(tr+s, tc, dr, dc, s);  
    else            //不在，将该子棋盘右上角的方块视为特殊方块  
    {  
        board[tr+s][tc+s-1]=t;  
        chessBoard(tr+s, tc, tr+s, tc+s-1, s);  
    }  
    //检查特殊方块是否在右下角子棋盘中  
    if (dr>=tr+s && dc>=tc+s )                //在  
        chessBoard(tr+s, tc+s, dr, dc, s);  
    else         //不在，将该子棋盘左上角的方块视为特殊方块  
    {  
        board[tr+s][tc+s] = t;  
        chessBoard(tr+s, tc+s, tr+s, tc+s, s);  
    }  
}  
  
int main()  
{  
    int  k; 
    int size = 1;   
    cin >> k; 
    for (int i = 0; i < k; i++)
    {
        size = size * 2;
    }
    int dr,dc;    
    cin >> dr >> dc;  
    chessBoard(0, 0, dr, dc, size);  
    for (int i = 0; i < size; i++)  
    {  
        for (int j = 0; j < size; j++){
            printf("%3d",board[i][j]);
        }    
        cout << endl;   
    }
	
}

3.8 快速排序

题目描述

给你一个整数数组nums，请你将该数组升序排列(要求使用快速排序)。

输入格式

第一行输入数组元素个数
第二行输入各数组元素

输出格式

排序后的数组

样例

输入样例 1

1
2

4
5 2 3 1

输出样例 1

1 2 3 5

输入样例 2

1 2	6 5 1 1 2 0 0

输出样例 2

1	0 0 1 1 2 5

代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> nums;

void Swap(vector<int> &result, int low, int high)
{
    int tmp = result[low];
    result[low] = result[high];
    result[high] = tmp;
}
//先选取一个值作为枢轴值，然后想尽办法将它放到一个位置，
//使得它左边的值都比他小，右边的值都比它大，最后返回该枢轴所在位置。
int Partition(vector<int> &result, int low, int high)
{
    int pivotkey = result[low]; //取第一个元素作为枢轴值
    while (low < high)
    {
        //从result的两端交替向中间扫描
        //整个过程要保证high指针后面的值都比枢轴值大；low指针前面的值都比枢轴值小
        while (low < high && result[high] >= pivotkey)
        {
            high--;
        }
        Swap(result, low, high); //将比枢轴值小的交换到低端
        while (low < high && result[low] <= pivotkey)
        {
            low++;
        }
        Swap(result, low, high); //将比枢轴值大的交换到高端
    }

    return low; //返回枢轴所在位置（最终时刻low和high指向同一个位置）
}

void Qsort(vector<int> &result, int low, int high)
{
    if (low < high)
    {
        //将result[low, ..., high]一分为二，返回枢轴所在位置
        int pivot = Partition(result, low, high);
        Qsort(result, low, pivot - 1);  //左半部分
        Qsort(result, pivot + 1, high); //右半部分
    }
}



int main()
{
    int n = 0;
    cin >> n;
    for (int tem = 0; cin >> tem;)
    {
        nums.push_back(tem);
        if (cin.get() == '\n')
        {
            break;
        }
    }
    vector<int> result(nums);
    int low = 0;
    int high = result.size() - 1;
    Qsort(result, low, high);
    for (int i = 0; i < n; i++)
    {
        cout << result[i] << " ";
    }
    return 0;
}

3.9 归并排序

题目描述

给你一个整数数组nums，请你将该数组升序排列

输入格式

一个整数，表示数组元素个数
一行整数，表示整数数组中各元素

输出格式

一行整数，表示排序后的数组元素

样例

输入样例 1

1
2

4
5 2 3 1

输出样例 1

1 2 3 5

输入样例 2

1 2	6 5 1 1 2 0 0

输出样例 2

1	0 0 1 1 2 5

代码

#include <iostream>
#include <vector>
using namespace std;

vector<int> nums;
vector<int> tmp;

void mergeSort(vector<int> &nums, int left, int right)
{
    if (left >= right)
        return;
    //对一个长为n的待排序的序列，先将其分解成两个长度为n/2的子序列。
    int mid = (left + right) / 2;   
    //每次先递归调用函数使两个子序列有序，
    mergeSort(nums, left, mid);
    mergeSort(nums, mid + 1, right);
    int i = left, j = mid + 1;
    int cnt = 0;
    //然后我们再线性合并两个有序的子序列使整个序列有序。
    while (i <= mid && j <= right)
    {
        if (nums[i] < nums[j])
        {
            tmp[cnt++] = nums[i++];
        }
        else
        {
            tmp[cnt++] = nums[j++];
        }
    }

    while (i <= mid)
    {
        tmp[cnt++] = nums[i++];
    }
    while (j <= right)
    {
        tmp[cnt++] = nums[j++];
    }
    for (int i = 0; i < right - left + 1; i++)
    {
        nums[i + left] = tmp[i];
    }
}
int main()
{
    int n = 0;
    cin >> n;
    for (int tem = 0; cin >> tem;)
    {
        nums.push_back(tem);
        if (cin.get() == '\n')
        {
            break;
        }
    }
    int left = 0;
    int right = nums.size() - 1;
    tmp.resize((int)nums.size(), 0);
    mergeSort(nums, left, right);
    for (int i = 0; i < n; i++)
    {
        cout << nums[i] << " ";
    }
    return 0;
}

4. 动态规划

4.1 爬楼梯

题目描述

假设你正爬楼梯，需要n阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢？

输入格式

输入：2

输出格式

输出：2

样例

输入样例 1

输出样例 1

代码

#include<iostream>
using namespace std;
int climbStairs(int n){
    //动态规划
    int len = n + 1;
    int dp[len];
    dp[0] = 1;
    dp[1] = 1;
    if (n == 1 || n == 0)
    {
        return 1;
    }
    for (int i = 2; i < len; i++)
    {
        dp[i] = dp[i-1] + dp[i-2];    // 第n阶楼梯的方案可由第n-1和n-2阶楼梯方案之和求出，
                                      // 因为只可能从这两个楼梯才能到达第n阶楼梯
    }

    return dp[len - 1];
}

int main(){
    int n ;
    cin >> n;
    cout << climbStairs(n) << endl;
}

4.2 零钱兑换

题目描述

给你一个整数数组coins，表示不同面额的硬币；以及一个整数amount，表示总金额。计算并返回可以凑成总金额所需的最少硬币个数。如果没有任何一种硬币组合能组成总金额，返回-1。你可以认为每种硬币的数量是无限的。

输入格式

输入：coins={1,2,5},amount=11

输出格式

输出：3 解释：11=5+5+1

样例

输入样例 1

1
2

1 2 5
11

输出样例 1

输入样例 2

1
2

2
3

输出样例 2

-1

输入样例 3

1
2

1
0

输出样例 3

代码

#include<iostream>
#include<vector>
using namespace std;
int get_change(vector<int> coins, int amount){
    //因为凑成 amount 金额的硬币数最多只可能等于 amount（全用 1 元面值的硬币），`
	//定义(amount + 1)个整型元素的向量,且给每个元素的初值为-1
	vector <int> dp(amount + 1, -1);    // dp(i) 为组成金额 i 所需的最少的硬币数量
	dp[0] = 0;
    for (int j = 0; j < coins.size(); j++)   // 第j种硬币
    {
        for (int i = coins[j]; i <= amount; i++){
            //如果dp[i - coins[j]]是有解的才能接着往下进行 
            if (dp[i - coins[j]] != -1 && (dp[i] == -1 || dp[i] > dp[i - coins[j]] + 1)) 
            {
                dp[i] = dp[i - coins[j]] + 1;   //组成金额 i 所需的最少硬币数量 = 组成金额 i-coins[j]所需的最少硬币数量 + 1
            }
        }
    }
    return dp[amount];
}
int main(){
    int amount = 0;
    vector<int> coins;
    for(int temp = 0; cin >> temp;)
    {
        coins.push_back(temp); //将输入的值push到容器的尾端
        if (cin.get() == '\n')
        break;
    }
    cin >> amount;
    cout << get_change(coins, amount) << endl;
     
}

4.3 最长公共子序列

题目描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

输入格式

输入：text1 = “abcde”, text2 = “ace”

输出格式

输出：3

样例

输入样例 1

1
2

abcde
ace

输出样例 1

代码

#include<iostream>
#include<cstdio>
#include<math.h>
using namespace std;

int main(){
    string text1,text2;
    int count[256][256];
    int len1,len2 = 0;
    cin >> text1 >> text2;
    len1 = text1.length();
    len2 = text2.length();
    for (int i = 1; i <= len1; i++)
    {
        for (int j = 1; j <= len2; j++)
        {
            if (text1.at(i-1) == text2.at(j-1))  //string .at()用于获取指定字符，
            {                                    //at(i),i就是想要获取的字符的下标，函数返回值为指定的字符
                count[i][j] = count[i-1][j-1]+1;   //如果相等则在左斜上方的基础上+1
            }
            else
            {  //如果不相等 则写入 左边和上方 数值中大的一个 即写入之前的历史
                count[i][j] = max(count[i][j-1],count[i-1][j]);
            }
        
        }
    }
    cout << count[len1][len2] << endl;    //二维数组的最后一个值即为结果
}

4.4 石子游戏

题目描述

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。亚历克斯和李轮流进行，亚历克斯先开始。每回合，玩家从行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

输入格式

输入：5 3 4 5

输出格式

true

样例

输入样例 1

5 3 4 5

输出样例 1

true

代码

#include<iostream>
#include<vector>
using namespace std;


void stoneGame(vector<int>& stone) {
    int len = stone.size();
    vector<int> dp(stone);
    for(int i=len-2;i>=0;--i){
        for(int j = i + 1; j < len; ++j){
            dp[j] = max( stone[i]-dp[j], stone[j] - dp[j - 1] );
        }
    }
    if(dp[len - 1] > 0){
        cout << "true" ;
    }else{
        cout << "false" ;
    }
}


int main(){
    vector<int> stone;
    for (int i = 0;cin >> i;)
    {
        stone.push_back(i);
        if (cin.get() == '\n')
        break;
    }
    stoneGame(stone);
}

4.5 整数拆分

题目描述

给定一个正整数n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。

输入格式

输入：2

输出格式

输出：1

样例

输入样例 1

输出样例 1

代码

#include<iostream>
#include<algorithm>
using namespace std;

int split_Int(int n){
    int dp[n+1];  //dp[n]表示正整数n获得的最大乘积
    for (int i = 0; i < n+1; i++)   // 给数组初始化方便后面比较
    {
        dp[i] = 0;
    }
    
    dp[1] = 1;
    dp[2] = 1;
    for (int i = 2; i <= n; i++)
    {
        for (int j = 1; j <= (i/2); j++)     // j<=(i/2) 因为 1*(n-1) 和 (n-1) * 1是等价的
        {   
            dp[i] = max(dp[i], max(j * dp[i - j], j * (i - j)));  //采用循环遍历出 dp[i]所有的划分方法 然后将最大的值返回dp[i]
               
        }
        
    }
    return dp[n];
}

int main(){
    int n;
    cin >> n;
    int value = split_Int(n);
    cout << value << endl;
}

5. 回溯法

5.1 N皇后问题

题目描述

在一张N * NN∗N的国际象棋棋盘上，放置NN个皇后，使得所有皇后都无法互相直接攻击得到，（皇后可以直接攻击到她所在的横行，数列，斜方向上的棋子），现在输入一个整数NN，表示在NNN∗N的棋盘上放NN*个皇后，请输出共有多少种使得所有皇后都无法互相直接攻击得到的方案数。例如下面这样的摆法，是4皇后的一个解（1代表有皇后，0代表没有）

输入格式

一个整数NN

输出格式

能使得在NNN∗N的国际象棋棋盘上放置NN*个皇后，并且所有皇后都无法互相直接攻击得到的方案数

样例

样例输入1

样例输出1

样例输入2

样例输出2

数据范围与提示

1<=N<=13

代码


#include <stdio.h>
#include <stdlib.h>
#include <time.h>
const int N=13;   //最多放皇后的个数
int queen[N];         //各皇后所在的行号
int count = 0;     //统计解得个数

//检验第i行的k列上是否可以摆放皇后
int find(int i,int k) 
{
  int j=1;
  while(j<i)  //j=1~i-1是已经放置了皇后的行
  {
         //第j行的皇后是否在k列或(j,q[j])与(i,k)是否在斜线上
         if(queen[j]==k ||abs(j-i)==abs(queen[j]-k))
                return 0;
         j++;
  }
  return 1;
}
//放置皇后到棋盘上
void place(int k,int n) 
{
  int j;
  if(k>n)
         count++;
  else
  {
         for(j=1;j<=n;j++)   //试探第k行的每一个列
         {
            if(find(k,j))
            {
                queen[k] = j;
                place(k+1,n);  //递归
            }
         }
  }
}
 
int main(void)
{
  int n;
//   printf("请输入皇后个数：");
  scanf("%d",&n);
  place(1,n);
  printf("%d\n",count);
  return 0;
}

5.2 01背包问题

题目描述

给定n种物品和一背包。物品i的重量是wi>0，其价值为vi>0，背包的容量为c。问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？（要求使用回溯法）

输入格式

第一行输入物品数量和背包容量第二行输入所有物品重量第三行输入所有物品价值

输出格式

第一行输出最大价值第二输出放置方案

样例

输入样例 1

1
2
3

4 6
5 3 2 1
4 4 3 1

输出样例 1

1
2

8
0 1 1 1

代码

#include<iostream>
using namespace std;

int main()
{
	int n,v;
    cin >> n >> v;       // n 是物品的数量 v是背包容量
    int weight[n],value[n];
    for (int i = 0; i < n; i++)
    {
        cin >> weight[i];
    }
    for (int j = 0; j < n; j++)
    {
        cin >> value[j];
    }
    
	int maxValue[n + 1][v + 1];
    int restWeight[n + 1][v + 1];
    for (int i = 0; i < n+1; i++)    //数组初始化为0
    {
        for (int j = 0; j < v+1; j++)
        {
            maxValue[i][j] = 0;
            restWeight[i][j] = 0;
        }
        
    }
    
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= v; j++) {
            if (j < weight[i - 1])
            {
                maxValue[i][j] = maxValue[i - 1][j];
                restWeight[i][j] = restWeight[i - 1][j];
            } 
            else 
            {
                maxValue[i][j] = maxValue[i - 1][j - weight[i - 1]] + value[i - 1];
                restWeight[i][j] = i;
                if (maxValue[i - 1][j] >= maxValue[i][j]) {
                    maxValue[i][j] = maxValue[i - 1][j];
                    restWeight[i][j] = restWeight[i - 1][j];
                }
            }
        }
    }	
	cout << maxValue[n][v] << endl;
    int x[n];
    for (int i = 0; i < n; i++)   //数组初始化为0
    {
        x[i] = 0;
    }
    
    for (int i = n, j = v; i >= 1; i--) {
        if (restWeight[i][j] == 0)
        {
            break;
        }
        x[restWeight[i][j] - 1] = 1;
        j = j - weight[restWeight[i][j] - 1];
    }
    for (int i = 0; i < n; i++) 
    {
        cout << x[i] << " ";
    }
}

5.3 砝码称重

题目描述

小明捡到了一架没有游标的天平和N个标有重量的砝码，于是他想知道他能够称出多少种不同的重量（假设只能将砝码放在一侧）。

输入格式

输入的第一行包含一个正整数N，表示有N个砝码。接下来一行有N个正整数，表示N个砝码的重量。

输出格式

输出一行，包含一个整数，表示能够称出多少种不同的重量。

数据规模和约定

N<16,砝码重量<=1000

样例

输入样例 1

1
2

3
1 2 3

输出样例 1

代码

#include <iostream>
#include <numeric>		//数组求和accumulate()函数的头文件
#include <vector>
#include <set>			//利用set去重
using namespace std;

vector<int> FM_Weight;	    // 存储砝码重量
set<int> ans;				//存储结果
vector<int> route;       //存储递归时当前路径

//即当前路径求和,S_Index标记起始位置
void Solution(int n,int S_Index)
{
	// start == n 表示遍历结束 
	if (S_Index == n)
		return;

	for (int i = S_Index;i < n;i++)
	{
		route.push_back(FM_Weight[S_Index]);					//把当前结点加入路径
		ans.insert(accumulate(route.begin(), route.end(), 0));	//对结点求和										 							
        S_Index++;
		Solution(n, S_Index);							//递归调用  此时索引值 +1 
		route.pop_back();									//回溯
	}

}


int main()
{
	int n;
	cin >> n;
    int value;
	for (int i = 0; i < n; i++)
    {
        cin >> value;
        FM_Weight.push_back(value);
    }
    
    // for (int i = 0; i < n; i++)
    // {
    //     cout << FM_Weight[i] << endl;
    // }
    
	Solution(n,0);
	cout << ans.size() <<  endl;
	return 0;
}

5.4 方格填数

题目描述

如下的10个格子，填入0~9的数字。要求：连续的两个数组不能相邻。（左右、上下、对角都算相邻），一共有多少种可能的填数方案？

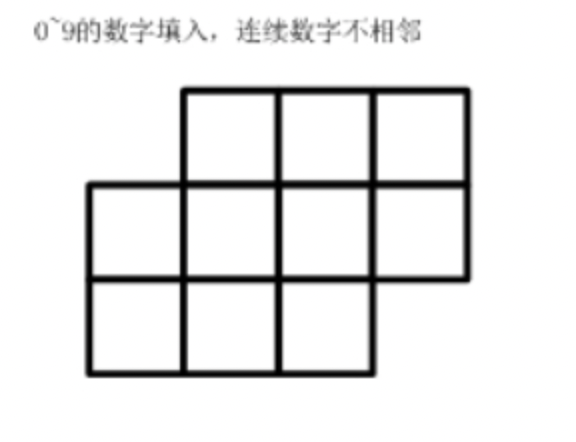
输入格式

无输入

输出格式

一个整数

代码

#include <iostream>
#include <algorithm> //next_permutation()函数
#include <cmath>

using namespace std;
int num = 0;
/*
用四个循环 左右检测 上下检测 左斜检测 右斜检测==1的话返回0
在主函数里面if检测 上面四个循环的返回值
*/
int Solution(int *a, int n)
{
    int i;

    for (i = 0; i < 9; i++)
    {
        if (abs(a[i] - a[i + 1]) == 1 && i != 2 && i != 6)
            return 0;
    }
    for (i = 0; i < 6; i++)
    {
        if (abs(a[i] - a[i + 4]) == 1)
            return 0;
    }
    for (i = 0; i < 7; i++)
    {
        if (abs(a[i] - a[i + 3]) == 1 && i != 3)
            return 0;
    }
    for (i = 0; i < 5; i++)
    {
        if (abs(a[i] - a[i + 5]) == 1 && i != 2)
            return 0;
    }
    return 1;
}

int main()
{
    int a[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
    int n = 10;
    do
    {
        if (Solution(a, n) == 1)
        {
            num++;
        }
        // next_permutation()是一个bool函数，
        //作用是传入一个数组，输出这个数组的后一个排序
        // next_permutation(begin,end)
        //当前序列不存在下一个排列时，函数返回false，否则返回true。
    } while (next_permutation(a, a + n));
    cout << num;
    return 0;
}

5.5 简单装载问题

题目描述

有n个集装箱要装上一艘载重量为W的轮船，其中集装箱i(1≤i≤n)的重量为Wi。

不考虑集装箱的体积限制，现要从这些集装箱中选出重量和小于等于W并且尽可能大的若干装上轮船。例如，n=5，W=10，w={5，2，6，4，3}时，其最佳装载方案是(1,1,0,0,1)或者(0,0,1,1,0),即装载的集装箱重量和达到最大值10。采用回溯法求解。

输入格式

第一行输入集装箱个数n和轮船的载重量

第二行输入集装箱的重量

输出格式

输出所有的可行方案，每个方案单独占一行

样例

输入样例 1

1 2	5 10 5 2 6 4 3

输出样例 1

1 2	1 1 0 0 1 0 0 1 1 0

代码

#include<iostream>
using namespace std;
int maxw = 0;   // 装载的总重量
int op[100];    // 存放最优解向量

void Print_Out(int n, int op[]){
    for (int i = 0; i < n; i++)
    {
        cout << op[i] << " ";
    }
    cout << endl;	
}
void Solution(int i, int tw, int rw, int n, int W, int container[], int op[])
{
    
    if (i >= n)
    {
        if (tw >= maxw)
        {	
            maxw = tw;
            Print_Out(n, op);
        }
    }
    else
    {
        if (tw + container[i] <= W)      //左剪枝
        {
            op[i] = 1;                   //选择货物
            Solution(i + 1, tw + container[i], rw - container[i], n, W, container, op);
        }
        if (tw + rw - container[i] > maxw)//右剪枝
        {
            op[i] = 0;                    //不选择货物
            Solution(i + 1, tw, rw - container[i], n, W, container, op);
        }
        
    }
}

int main(){ 
    int n,W;
    cin >> n >> W;
    int container[n];
    int rw;  
    for (int i = 0; i < n; i++)
    {
        cin >> container[i];
    }

    for (int i = 0; i < n; i++)
    {
        rw += container[i];
    }
    Solution(0, 0, rw, n, W, container, op);
    
}

5.6 求解子集和问题

题目描述

给定n个不同的正整数集合w={w1, w2,…….wn} 和一个正整数W，要求找出w的子集s，使该子集中所有元素的和为W。例如，当n=4时，w={11，13，24，7}，W=31，则满足要求的子集为(11,13,7)和(24,7)。

输入格式

第一行输入n的个数和子集和W的值

第二行分别输入n个元素的值

输出格式

按行输出每个解

样例

输入样例 1

1 2	4 31 11 13 24 7

输出样例 1

1 2	11 13 7 24 7

代码

#include <iostream>
using namespace std;

int ans[100];    //用来存放解

int Print_out(int ans[], int num[], int n){
    for (int i = 0; i < n; i++)
    {
        if (ans[i] == 1)
        {
            cout << num[i] << " ";
        }
        
    }
    cout << endl;
    return 0;
}
// i 表示第i个整数
//tw表示第i个整数时选取的整数和
//rw为剩下的整数和
// n表示整数数量
// num[] 输入的数组
// W 目标和
// ans[]存放答案的数组
void Solution(int i, int tw, int rw, int n, int num[], int W, int ans[])
{
    if (i >= n)     //找到一个叶子结点
    {
        if (tw == W) 	//找到一个满足条件的解输出
        {
            Print_out(ans, num, n);
        }
    }
    else				//尚未找完所有整数 	
    {
        if (tw + num[i] <= W)		//左孩子结点剪枝：选取满足条件的整数w[i]
        {   
            ans[i] = 1;            //选取第i个整数 
            Solution(i+1, tw+num[i], rw-num[i], n, num, W, ans);
        }
        if (tw + rw > W)        //右孩子结点剪枝：剪出不可能存在解的结点
        {
            ans[i] = 0;          //不选取第i个整数，回溯 
            Solution(i+1, tw, rw-num[i], n, num, W, ans);
        }
        
    }
}



int main()
{
    int W, n;
    cin >> n >> W;
    int num[n];
    int rw = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> num[i];
    }
    
    for (int j = 0; j < n; j++)   //求所有整数和
    {
        rw += num[j];
    }
    Solution(0, 0, rw, n, num, W, ans);

}

5.7 全排列问题

题目描述

输出自然数 1 到 n所有不重复的排列，即 n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

第一行为一个整数n

输出格式

由1至n组成的所有不重复的数字序列，每行一个序列。每个数字之间由空格隔开

样例

输入样例 1

输出样例 1

代码

#include <iostream>
#include <cstdio>
using namespace std;
bool flag[100];   //标记位 表示这个数字是否用到过
int ans[100];
int n;


void Solution(int con)   
{
    if (con == n+1)   // 当con == n+1的时候证明已经遍历结束
    {
        for (int i = 1; i <= n; i++)
        {
            cout << ans[i] << " ";
        }
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++)
    {//每次判断数字是否之前便使用过，如果没有使用过，即选择这个数字 flag[]=1，
        if (flag[i] == 0) 
        {
            flag[i] = 1;
            ans[con] = i;
            //继续调用Solution，在Solution之后，把这个数字重新还原以便下次使用
            Solution(con + 1);
            flag[i] = 0;
        }
    }
}
int main()
{
    cin >> n; 
    Solution(1);
    return 0;
}

本文采用CC-BY-SA-3.0协议，转载请注明出处
作者: Lee

鲨鱼辣椒

【笔记】算法实验课题目汇总

1. 贪心法

1.1 快乐司机

题目描述

输入格式

输出格式

样例

样例输入

样例输出

数据范围与提示

解释：

范围

代码

1.2 活动安排

输入格式

输出格式

样例

输入样例 1

输出样例 1

数据范围与提示

代码

1.3 分发饼干

题目描述

输入格式

输出格式

样例

数据范围与提示

代码

2. 蛮力法

2.1 狱卒问题

题目描述

输入格式

输出格式

样例

输入样例1

输出样例1

输入样例2

输出样例2

数据范围与提示

代码

2.2 四平方和

题目描述

输入格式

输出格式

样例

代码

2.3 求n以内的所有素数

输入格式

输出格式

样例

输入样例

输出样例

代码

2.4 找零问题

题目描述

输入格式

输出格式

样例

样例输入1

样例输出1

样例输入2

样例输出2

样例输入3

样例输出3

代码

2.5 最长公共子串

题目描述

输入格式

输出格式

样例

输入样例 1

输出样例 1

数据范围与提示

代码

3. 分治法

3.1 最大子段和

题目描述

输入格式

输出格式